Kürzeste Pfadwege
Was sind kürzeste Pfadwege?
Kürzeste Pfadwege sind ein zentraler Bestandteil der Graphentheorie und dienen dazu, den kürzesten Weg zwischen zwei Punkten (Knoten) in einem Netzwerk oder Graphen zu finden. Diese Algorithmen werden in verschiedenen Anwendungsbereichen eingesetzt, zum Beispiel in Navigationssystemen, Logistik, Telekommunikation und sogar in sozialen Netzwerken.
Ein bekannter Algorithmus zur Berechnung kürzester Pfade ist der Dijkstra-Algorithmus. Dieser wurde von Edsger Dijkstra entwickelt und hilft dabei, in einem gewichteten Graphen den kürzesten Weg von einem Startpunkt zu allen anderen Knoten zu finden. Die Kantengewichte repräsentieren dabei die "Kosten" oder Entfernungen zwischen den Knoten.
Wann braucht man kürzeste Pfadwege?
Die Berechnung von kürzesten Pfadwegen wird in vielen Bereichen benötigt, zum Beispiel:
- Navigation: Routenberechnung in GPS-Systemen, um den schnellsten oder kürzesten Weg von einem Punkt zum anderen zu finden.
- Logistik: Optimierung von Lieferwegen für Waren und Ressourcen.
- Telekommunikation: Finden von optimalen Verbindungen in Netzwerken.
- Soziale Netzwerke: Bestimmung von Verbindungen und Abständen zwischen Personen oder Interessen.
Dijkstra-Algorithmus
Der Dijkstra-Algorithmus hilft dabei, den kürzesten Weg von einem Startpunkt zu einem Zielpunkt in einem Netzwerk zu finden, indem er alle möglichen Routen untersucht und die mit den geringsten "Kosten" auswählt. Hier sind die grundlegenden Schritte:
- Startpunkt festlegen: Wählen Sie einen Startknoten aus, von dem der kürzeste Weg gefunden werden soll.
- Entfernungen berechnen: Berechnen Sie die Entfernungen von diesem Startpunkt zu allen benachbarten Knoten.
- Kürzesten Pfad auswählen: Wählen Sie den Knoten mit der geringsten Entfernung als nächsten Schritt aus und wiederholen Sie den Prozess.
- Wiederholen: Aktualisieren Sie die Entfernungen nach jedem Schritt und wiederholen Sie den Vorgang, bis das Ziel erreicht ist.
Anwendung an einem Beispiel
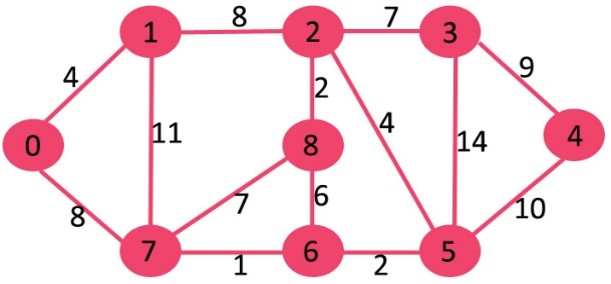
Lernvideo
Schauen Sie sich das Lernvideo an, um den Dijkstra-Algorithmus in Aktion zu sehen:
Übungen
Laden Sie sich die Übungsvorlage herunter, um die Konzepte des Dijkstra-Algorithmus selbst zu üben:
Übungsvorlage für Dijkstra-Algorithmus herunterladen