Einführung in Sortieralgorithmen
Sortieralgorithmen sind in der Informatik von entscheidender Bedeutung, da sie dazu verwendet werden, eine gegebene Menge von Daten oder Elementen in eine bestimmte Reihenfolge zu bringen. Diese Reihenfolge kann auf verschiedene Weisen definiert sein, je nach den Anforderungen eines bestimmten Problems. Eine der häufigsten Anwendungen von Sortieralgorithmen besteht darin, Daten in aufsteigender oder absteigender Reihenfolge anzuordnen. Dies erleichtert das Suchen nach bestimmten Elementen in den Daten erheblich. Sortieralgorithmen ermöglichen es, Statistiken über Daten leichter zu berechnen. Zum Beispiel ist es einfacher, den Median oder das Quartil in sortierten Daten zu finden.
In der Datenvisualisierung ist es oft erforderlich, Daten in einer bestimmten Reihenfolge anzuordnen, um Diagramme oder Grafiken korrekt darzustellen. Sortierte Daten können zur Datenanalyse und -verarbeitung effizienter verarbeitet werden. Dies ist besonders wichtig in Anwendungen wie Datenbankabfragen (SQL) und oder Big Data-Analysen. Sortieralgorithmen werden häufig verwendet, um Daten in einer bestimmten Reihenfolge für die Ausgabe vorzubereiten. Es gibt viele verschiedene Sortieralgorithmen, die in der Informatik verwendet werden, darunter bekannte Algorithmen wie Bubble Sort, Insertion Sort, Merge Sort, Quick Sort und Heap Sort. Die Wahl des richtigen Sortieralgorithmus hängt von verschiedenen Faktoren ab, einschließlich der Größe der Datenmenge.
Bubble-Sort-Algorithmus
Bubblesort ist der einfachste und gleich auch der älteste Sortieralgorithmus. Hier müssen einfach alle Elemente eines Arrays durchlaufen und miteinander verglichen werden. Wollen wir vom kleinsten zum größten Wert sortieren und ist ein Element größer als sein Nachfolger, werden diese Elemente getauscht. Damit ist Bubblesort ein stabiler, in-place Algorithmus.
Beim Bubblesort werden jeweils zwei aufeinanderfolgende Elemente miteinander verglichen und – wenn das linke Element größer ist als das rechte – werden diese vertauscht. Diese Vergleichs- und Tauschoperationen führt man von links nach rechts über alle Elemente durch, so dass nach dem ersten Durchlauf das größte Element ganz rechts positioniert ist. Diesen Prozess wiederholt man solange, bis es in einem Durchlauf zu keinem weiteren Vertauschen mehr kommt.
Die Laufzeitkomplexität beim Bubblesort ist im Best-Case O(n) und im Worst-Case O(n2), wobei n die Anzahl der zu sortierenden Elemente angibt.
Beispiel
Beispiel Formel: ((Anzahl der Element n) x (Anzahl der Iterationen)) x 1/2
Vereinfacht: 1/2 x (n2 - n)
Werte einsetzen: 1/2 x (72 - 7) = 1/2 x (49 - 7) = 1/2 x (42) = 21
Im obigen Beispiel sind 21 Vergleiche/Tausche notwendig, um die Zahlenreihe einmal umgekehrt aufsteigend zu sortieren.
Lernvideo zum Bubblesort Lernvideo
Insertion-Sort-Algorithmus
Der Insertionsort gehört in der Informatik zu den stabilen Sortieralgorithmen und kann als Sortieren durch Einfügen beschrieben werden, deswegen auch Einfügesortierenmethode genannt. Der Algorithmus ist stabil, arbeitet in-place und kann anhand eines Kartenspiels erläutert werden. Stell dir vor, du bekommst eine Karte nach der anderen gereicht. Du nimmst die erste Karte auf die Hand. Die zweite sortierst du dann links oder rechts davon ein. Die dritte je nach Größe links, dazwischen oder rechts und auch die folgenden Karten jeweils an der richtigen Stelle:
Die Laufzeitkomplexität beim Insertionsort ist im Best-Case O(n) und im Worst-Case O(n2), wobei n die Anzahl der zu sortierenden Elemente angibt.
Lernvideo zum Insertionsort Lernvideo
Merge-Sort-Algorithmus
Hier handelt es sich um einen der komplexeren Algorithmen. Mergesort gehört zur Klasse der "divide and conquer" Algorithmen. Um die Liste zu sortieren wird sie so oft halbiert bis nur noch einzelne Elemente übrig sind. Im Anschluss wird dann die Liste "gemerged". Das bedeutet, dass die vielen einzelnen "Listen", die wir hier nun haben, wieder zusammengesetzt und ihre Elemente an ihre korrekte Position gesetzt werden. Mergesort arbeitet stabil, arbeitet aber out-of-place und gehört damit zu den speicherintensiven Algorithmen. Dafür ist es ein sehr schneller Algorithmus, der auch problemlos mit großen, unsortierten Listen klarkommt. Mergesort funktioniert nach dem "Teile-und-herrsche"-Prinzip („divide and conquer“). Zunächst werden die zu sortierenden Elemente in zwei Hälften geteilt. Die entstandenen Sub-Arrays werden dann wieder geteilt – und wieder, bis Sub-Arrays der Länge 1 entstanden sind:
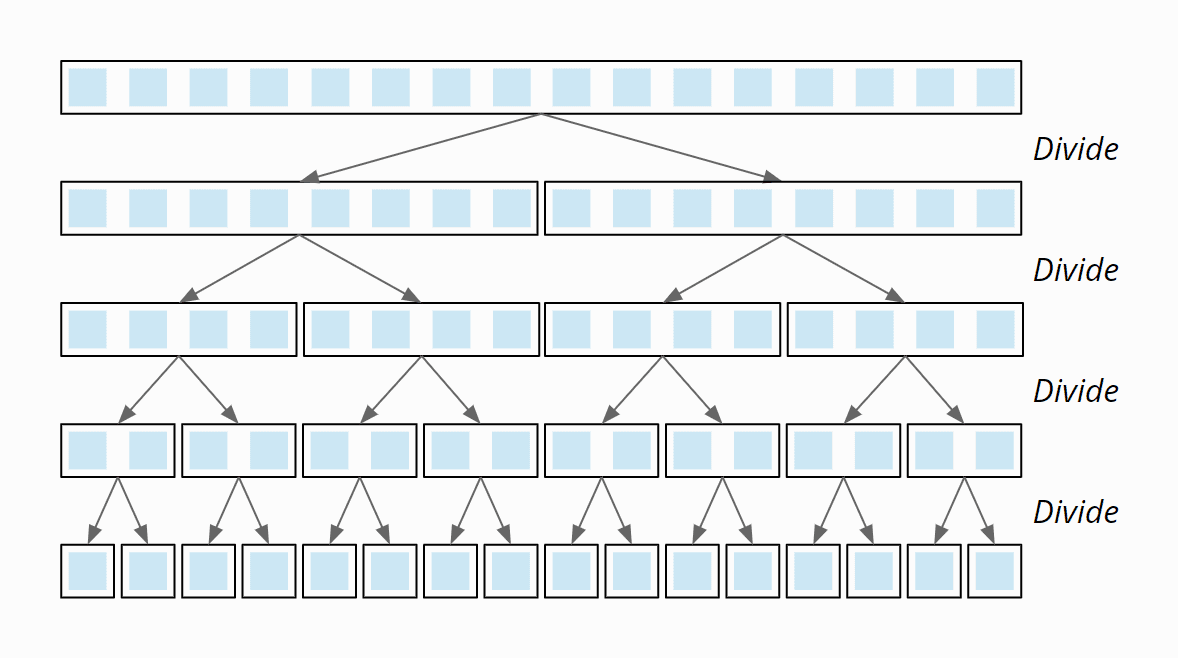
Nun werden in umgekehrter Richtung jeweils zwei Teil-Arrays so zusammengeführt ("gemerged"), dass jeweils ein sortiertes Array entsteht. Im letzten Schritt werden die zwei Hälften des ursprünglichen Arrays gemerged, so dass dieses letztendlich sortiert ist.
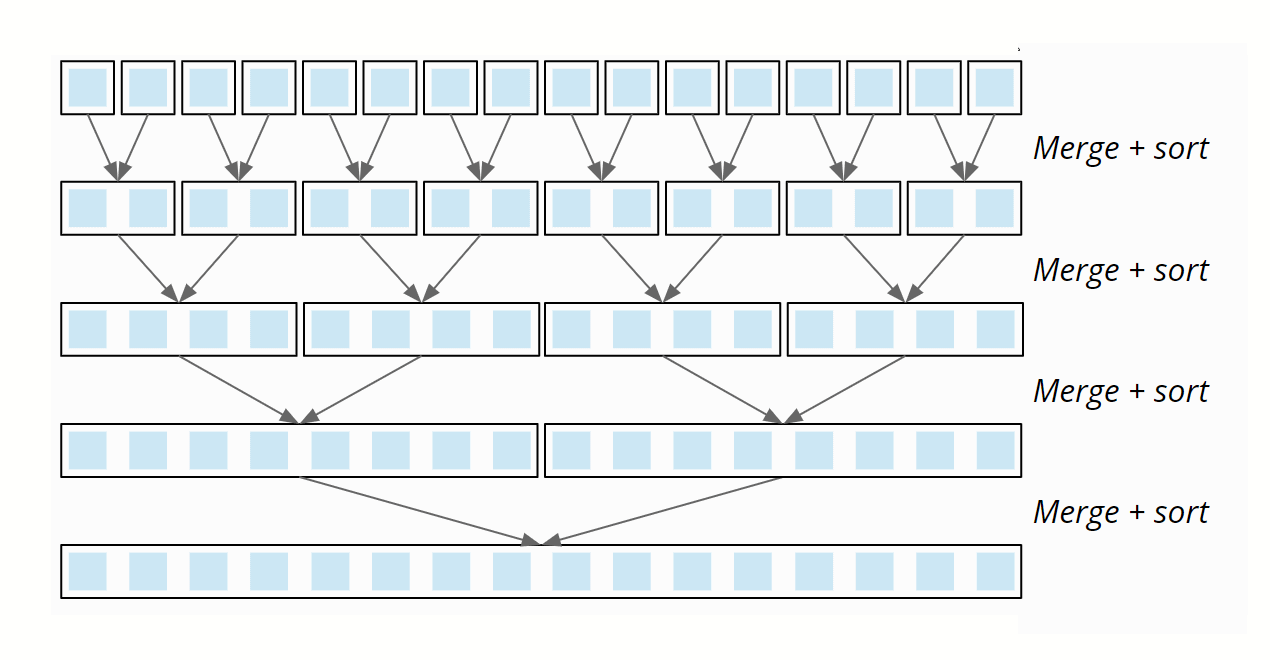
Die Laufzeitkomplexität beim Mergesort ist O(n log n).
Lernvideo zum Mergesort Lernvideo
Selection-Sort-Algorithmus
Selectionsort ist ziemlich einfach aufgebaut.
Das Einsortieren von Spielkarten auf die Hand ist eigentlich das klassische Beispiel für Insertionsort.
Selectionsort kann man im Grunde genommen auch mit Spielkarten darstellen.
Hier legt man zunächst alle Karten offen auf den Tisch.
Dann sucht man die kleinste Karte und nimmt sie nach links auf die Hand,
danach die nächst größere und setzt sie rechts daneben, usw. bis zuletzt die größte Karte aufgenommen und ganz rechts einsortierst ist.
Unterschied zu Insertionsort
Bei Insertionsort hatten wir die jeweils nächste unsortierte Karte genommen und dann in den sortierten Karten an der richtigen Stelle eingefügt ("inserted"). Selectionsort funktioniert gewissermaßen anders herum: Wir wählen ("select") die jeweils kleinste Karte aus den unsortierten Karten, um diese dann – eine nach der anderen – an die bereits sortierten Karten anzuhängen.
Dadurch das wir die Elemente direkt in der Liste tauschen, haben wir einen in-place Algorithmus, der die Reihenfolge der Elemente nicht erhält und damit instabil arbeitet.
Lernvideo zum Selectionsort Lernvideo
Die Laufzeitkomplexität beim Selectionsort ist im Best-Case, Worst-Case und Average O(n2), wobei n die Anzahl der zu sortierenden Elemente angibt.
Quick-Sort-Algorithmus
Quicksort ist das am häufigsten verwendete Verfahren. Es handelt sich dabei um einen instabilen, in-place Algorithmus. Grundlegend lässt sich sagen, dass man immer ein Element aus der Liste bestimmt, das sogenannte Pivotelement und dieses Element bildet dann den Maßstab für Vergleiche. Im Anschluss setzen wir alle anderen Elemente an ihre richtige Position. Die neuen Positionen bestimmt man immer auf Basis des Pivotelements. Wenn keine weiteren Elemente mehr zu sortieren sind, endet der Algorithmus.
Quicksort funktioniert nach dem "Teile-und-herrsche"-Prinzip ("divide and conquer"): Als erstes teilen wir die zu sortierenden Elemente auf zwei Bereiche auf – einen mit kleinen Elementen und einen mit großen Elementen. Welche Elemente klein sind und welche groß, entscheidet dabei das sogenannte Pivot-Element. Das Pivot-Element kann ein beliebiges Element aus dem Eingabe-Array sein.
Version 1 Lernvideo zum Quicksort Lernvideo Version 2 Lernvideo zum Quicksort Lernvideo
Die Laufzeitkomplexität beim Quicksort ist im: Best-Case: O(n log n) Average-Case: O(n log n) Worst-Case: O(n2), wobei n die Anzahl der zu sortierenden Elemente angibt.
Heap-Sort-Algorithmus
Ein "Heap" (deutsch: "Haufen" oder "Halde") bezeichnet einen Binärbaum, in dem jeder Knoten entweder größer/gleich seiner Kinder ist ("Max Heap") – oder kleiner/gleich seiner Kinder ("Min Heap").
Hier ist ein einfaches Beispiel für einen "Max Heap":
Die 9 ist größer als die 8 und die 5; die 8 ist größer als die 7 und die 2; usw. Ein Heap wird auf ein Array projiziert, indem dessen Elemente von oben links zeilenweise nach rechts unten in das Array übertragen werden:
Der oben gezeigte Heap sieht als Array also so aus:
Der Heapsort-Algorithmus besteht aus zwei Phasen: In der ersten Phase wird das zu sortierende Array in einen Max Heap umgewandelt. Und in der zweiten Phase wird jeweils das größte Element (also das an der Baumwurzel) entnommen und aus den restlichen Elementen erneut ein Max Heap hergestellt. Wie dies geschieht wird anhand der folgenden Zahlenfolge [3, 7, 1, 8, 2, 5, 9, 4, 6] erläutert. Wir "projizieren" das Array nun auf einen Binärbaum. Dabei ist der Binärbaum keine separate Datenstruktur, sondern lediglich ein Gedankenkonstrukt – im Speicher liegen die Elemente ausschließlich in dem Array.
Dieser Baum entspricht noch keinem Max Heap. Dessen Definiton lautet ja, dass Eltern immer größer oder gleich ihrer Kinder sind. Um einen Max Heap herzustellen, besuchen wir nun alle Elternknoten – rückwärts vom letzten bis zum ersten – und sorgen dafür, dass die Heap-Bedingung für den jeweiligen Knoten und die darunter erfüllt ist. Dies machen wir mit der sogenannten heapify()-Funktion.
Phase 1 Max-Heap erstellen - Aufruf Nr. 1 der heapify-Funktion
Die heapify()-Funktion wird zuerst für den letzten Elternknoten aufgerufen. Elternknoten sind 3, 7, 1 und 8. Der letzte Elternknoten ist die 8. Die heapify()-Funktion prüft, ob die Kinder kleiner sind als der Elternknoten. 4 und 6 sind kleiner als 8. An diesem Elternknoten ist die Heap-Bedingung also erfüllt, und die heapify()-Funktion ist beendet.
Aufruf Nr. 2 der heapify-Funktion
Aufruf Nr. 3 der heapify-Funktion
Nun wird heapify() auf der 7 aufgerufen. Kindknoten sind 8 und 2, nur die 8 ist größer als der Elternknoten. Wir tauschen also die 7 mit der 8:
Da der Kindknoten, den wir eben getauscht haben, selbst zwei Kinder hat, muss die heapify()-Funktion nun prüfen, ob die Heap-Bedingung für diesen Kindknoten noch erfüllt ist. In diesem Fall ist die 7 größer als 4 und 6, die Heap-Bedingung ist also erfüllt; die heapify()-Funktion ist damit beendet.
Aufruf Nr. 4 der heapify-Funktion
Jetzt sind wir bereits am Wurzelknoten mit dem Element 3 angekommen. Beide Kindknoten, 8 und 9 sind größer, wobei die 9 das größte Kind ist und daher mit dem Elternknoten vertauscht wird:
Wiederum hat der getauschte Kindknoten selbst Kinder, so dass wir die Heap-Bedingung an diesem Kindknoten überprüfen müssen. Die 5 ist größer als die 3, d. h. die Heap-Bedingung ist nicht erfüllt und muss durch Tauschen der 5 und der 3 wiederhergestellt werden:
Damit ist auch der vierte und letzte Aufruf der heapify()-Funktion beendet. Ein Max Heap ist entstanden:
Phase 2 - sortieren des Arrays
In Phase 2 machen wir uns die Tatsache zunutze, dass das größte Element des Max Heaps immer an dessen Wurzel (bzw. im Array ganz links) steht.
Root und letztes Element tauschen
Das Wurzelelement (die 9) tauschen wir nun mit dem letzten Element (der 6), so dass die 9 an ihrer finalen Position am Ende des Arrays steht (im Array blau markiert). Außerdem entfernen wir dieses Element gedanklich aus dem Baum (im Baum grau dargestellt):
Um die Heap-Bedingung wiederherzustellen, rufen wir die aus Phase 1 bekannte heapify()-Funktion auf dem Wurzelknoten auf. Wir vergleichen also die 6 mit ihren Kindern, 8 und 5. Die 8 ist größer, wir tauschen sie daher mit der 6:
Der getauschte Kindknoten hat wiederum zwei Kinder, die 7 und die 2. Die 7 ist größer als die 6, daher tauschen wir auch diese zwei Elemente:
Der getauschte Kindknoten hat auch noch ein Kind, die 4. Die 6 ist größer als die 4, die Heap-Bedingung ist an diesem Knoten also erfüllt, so dass die heapify()-Funktion beendet ist und wir wieder einen Max Heap haben:
Ergibt:
Wiederholen der Schritte bis...
Dieses ist das kleinste und verbleibt am Anfang des Arrays. Der Algorithmus ist beendet, das Array ist sortiert:
Die Laufzeitkomplexität beim Heapsort beträgt (n log n)