Der Huffman-Code
Der Huffman-Algorithmus stellt eine Methode zur verlustfreien Komprimierung von Daten dar. Er wurde 1952 von David A. Huffman entwickelt. Der Algorithmus erzeugt aus Symbolen und deren Verteilung im zu komprimierenden Text, Binärbäume, aus welchen präfixfreie Codierungen variabler Länge (Huffman-Codes) gewonnen werden. Diese codieren den Text mit minimalem Speicherplatz. Die Codierung muss verlustlos sein, d.h. die Nachricht muss eindeutig und ohne Verlust von Information decodiert werden können. Häufig vorkommende Buchstaben werden mit kürzeren Codewörtern codiert, selten vorkommende Buchstaben können längere Codewörter haben.
Ein Algorithmus zur Huffman-Codierung könnte folgendermaßen aussehen: I. Initialisierung: Alle Zeichen werden Knoten zugeordnet und nach ihrer Häufigkeit in einer Liste sortiert. II. Solange die Liste der Knoten noch mehr als ein Element enthält:
(a) Entnehme die beiden Elemente mit der geringsten Häufigkeit der Liste und erzeuge einen Elternknoten hierfür. (b) Weise die Summe der Häufigkeiten der Kinder dem Elternknoten zu und füge diesen Knoten der Liste zu. (c) Den Zeigern des Elternknoten wird der Code 0, 1 zugeordnet (Reihenfolge im Prinzip beliebig).
Der Baum wird ausgehend von den Blättern bottom-up aufgebaut:
I. Trage die Buchstaben in die Blätter ein. Deren Häufigkeiten kannst du unter das jeweilige Blatt schreiben. II. Fasse die beiden vaterlosen Blätter mit den geringsten Häufigkeiten in einem Vaterknoten zusammen und addiere die Häufigkeiten der Kinder. Trage die Summe im Vaterknoten ein. III. Führe das Verfahren fort, stets die beiden Blätter (Buchstaben) bzw. Vaterknoten mit den geringsten Häufigkeiten zu einem weiteren Knoten zusammenzuführen und die Summe einzutragen, bis es nur noch einen vaterlosen Knoten gibt (die Wurzel). IV. Den linken Kanten wird je eine 0, den rechten je eine 1 zugewiesen (Reihenfolge im Prinzip beliebig).
Schauen wir es uns an einem Beispiel von Alice und Bob an: „ABRAKADABRA". Wir wissen, dass die Buchstaben mit gewissen Häufigkeiten vorkommen und stellen daraus eine Häufigkeitstabelle (Häufigkeitsanalyse) auf:
| Buchstabe | Häufigkeit |
|---|---|
| A | 5 |
| B | 2 |
| D | 1 |
| K | 1 |
| R | 2 |
Schritt 1: Es werden die Buchstaben und ihre Häufigkeiten in die bzw. unter die Blätter eingetragen.
Schritt 2: Es gibt noch vaterlose Knoten: A, B, K, D und R. Fasse die beiden vaterlosen Blätter mit den geringsten Häufigkeiten (K und D haben beide den Wert 1) in einem Vaterknoten zusammen, indem die Häufigkeiten der Kinder addiert werden. Trage die Summe 2 im Vaterknoten ein.
Schritt 3: Es gibt noch vaterlose Blätter: A, B, R. Fasse die zwei Knoten mit den geringsten Häufigkeiten in einem Vaterknoten zusammen (z.B. den Vaterknoten mit dem Wert 2 und Blatt B mit dem Wert 2) und addiere die Häufigkeiten der Kinder. Trage die Summe 4 im Vaterknoten ein.
Schritt 4: Es gibt noch einen vaterlosen Blatt: A. Fasse aber zuerst die Knoten mit den geringsten Häufigkeiten zusammen, den Vaterknoten mit dem Wert (BR 4) und DK mit dem Wert 2 in einem Vaterknoten zusammen und addiere die Häufigkeiten der Kinder. Trage die Summe 6 im Vaterknoten ein.
Schritt 5: Füge nun Blatt A zum Vaterknoten (BDKR). Summiere die Häufigkeiten (den Vaterknoten mit dem Wert 6 und das Blatt A mit Wert 5) in einem Vaterknoten zusammen und addiere die Häufigkeiten der Kinder. Trage die Summe 11 im Vaterknoten ein.
Schritt 6: Die Codierung der Buchstaben aus dem Huffman-Baum ablesen Es gibt kein vaterloses Blatt mehr und noch genau einen vaterlosen Knoten (die Wurzel). Den linken Kanten wird je eine 0, den rechten je eine 1 zugewiesen. Nun kann man die Codierung für die verschiedenen Buchstaben ablesen. Starte bei der Wurzel und folge den Kanten bis zu einem Blatt. Schreibe 0 auf, wenn du nach links gehst und 1, wenn du nach rechts gehst. Codewort für „A“ bestimmen: Von der Wurzel gehst du erst nach links und erreichst Blatt „A“. Du bist einmal nach links gegangen, also ist das Codewort für „A“ gleich „0“. Somit kann man gleichzeitig auch die sogenannte Code-Tabelle erstellt werden.
Die Codierung von „ABRAKADABRA" lautet:
Zusammenfassung des Algorithmus
1. Häufigkeitstabelle aufstellen. 2. Erstelle die Huffman-Liste. 3. Wiederhole die Zusammenführung der beiden mit der geringsten Häufigkeit beschrifteten Bäume so lange, bis die Huffman-Liste nur noch aus einem Baum, dem Huffman-Baum, besteht. 4. Schreibe an den linken Kanten je eine 0n und an den rechten Kanten eine 1 auf. (Reihenfolge im Prinzip beliebig).
Dekodierung
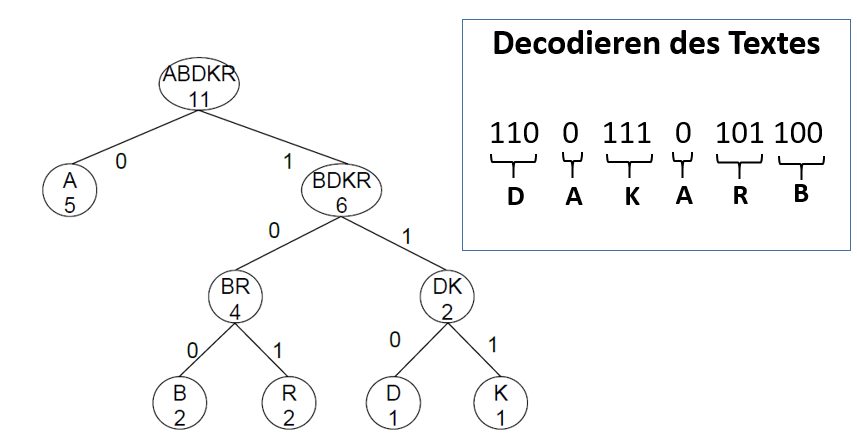
Was passiert nun, wenn Bob eine codierte Nachricht von Alice erhält und diese decodieren will? Um sie decodieren zu können, muss Bob natürlich wissen, wie der Huffman-Baum aussieht, ansonsten weiss er nicht, wie Alice codiert hat. Er geht Bit für Bit durch das codierte Wort und geht den Baum wie folgt:
1. Starte bei der Wurzel. 2. Wenn eine 0 im codierten Wort ist, gehe nach links. 3. Wenn eine 1 im codierten Wort ist, gehe nach rechts. 4. Angekommen bei einem Blatt, schreibe den Buchstaben im Blatt auf und beginne wieder bei der Wurzel (bei 1.).